Beyond Keywords: The Power of Vector Databases – Bioinformatics | Algorithms | Coding | Simplifying Bioinformatics for Curious Minds

How it all started

I’ve recently been exploring vector databases—through tutorials, articles, and introductory courses. The learning curve felt math-heavy at first, but once the concepts fell into place, things became surprisingly clear.

One important lesson stood out: exact keyword matching is no longer enough. Traditional search methods that rely only on keywords have lost their effectiveness. Modern users expect search to capture context and meaning, not just strings of text.

That’s where vector databases come in. In this blog, I’ll share what I’ve learned so far in plain English—breaking down the concepts in a way that’s easy to follow.

✍️Vector databases are the secret sauce behind search systems that feel almost human.

✍️Vector databases power the shift from keyword search to semantic search—where results are based on meaning, not just words.

What Is a Vector Database?

Imagine walking into a giant candy store. There are thousands of sweets—gummy bears, chocolate bars, lollipops, sour worms. Now, suppose you want candies similar to your favorite strawberry lollipop. You don’t want random candy—you want ones that taste fruity and sweet, maybe like cherry lollipops.

A vector database is like this candy store—but for information. Instead of organizing by name or type, it groups things by similarity. And instead of candies, it stores text, images, or sounds, all converted into vectors (lists of numbers).

The Concept of Embeddings

Here’s the fun part: computers can’t actually taste candy. So how do they know what’s similar?

That’s where embeddings come in. They’re like flavor codes in numbers that capture meaning.

✨ Example:

Strawberry lollipop → [0.9, 0.1, 0.3, 0.7]
Cherry lollipop → [0.8, 0.2, 0.4, 0.6]

These codes are close, so the computer says: “Both fruity and sweet!”

But a chocolate bar → [0.2, 0.9, 0.8, 0.1] looks totally different, so the computer knows it’s rich and creamy, not fruity.

What Do Embeddings Do?

Embeddings turn words, pictures, or sounds into number-codes so computers can:

Find similar images (like cats that look alike )
Translate languages (“hello” ↔ “hola”)
Recommend songs or movies you’ll enjoy
Answer questions even when you don’t use the exact words

In short: embeddings help computers understand meaning.

What Is a Vector?

In mathematics, a vector is simply an ordered list of numbers.

Examples:

2D vector: [3, 4] (a point on a plane).
3D vector: [1, -2, 5] (a point in space).

So a vector is just a container of numbers—it doesn’t mean anything by itself.

Vectors vs Embeddings

A vector = any list of numbers.
An embedding = a vector with meaning, built to represent information.

Example:

“Cat” → [0.12, -0.87, 0.44, …]
“Dog” → a nearby vector, since they’re related.

✍️ Every embedding is a vector, but not every vector is an embedding.

✨ Another Example (Text)

Word: “apple” → Embedding: [0.21, -0.35, 0.77, ...]
Word: “banana” → Embedding: [0.25, -0.40, 0.72, ...]
Word: “car” → Embedding: [0.90, 0.10, -0.50, ...]

Here “apple” and “banana” embeddings will be closer together than “apple” and “car” because they’re both fruits.

✅ In short:

Vector = mathematical object (list of numbers).
Embedding = vector with meaning (used to represent real-world objects in a way computers can compare and understand).

How Do Embeddings Work?

Let’s break it down step by step:

Start with Raw Data
You begin with something like text, an image, or even audio.

Convert Data into Embeddings
The raw data is passed through an embedding model (like BERT for text, CLIP for images, or Whisper for audio). The model transforms it into a vector embedding — essentially a list of numbers such as:
[0.12, -0.87, 0.33, ...]

Store in a Vector Database
These embeddings, along with their metadata (like file name, description, or ID), are stored inside a vector database.

Handle a Query
When a user enters a query (text, image, or audio), the same embedding model converts that query into its own vector.

Find Similar Vectors (ANN Search)
The query vector is compared against stored vectors using Approximate Nearest Neighbor (ANN) algorithms such as HNSW, IVF, or LSH. These algorithms quickly locate vectors that are closest in meaning to the query.

Return the Most Similar Items
Finally, the system returns the items most similar to the query — not by exact keyword matches, but by semantic similarity.

Here’s a simple diagram to show the whole process:

[ Raw Data: Text | Image | Audio ]
                ↓
        ┌────────────────────┐
        │  Embedding Model   │  ← (e.g., BERT, CLIP, Whisper)
        └────────────────────┘
                ↓
     [ Vector Embedding: e.g., [0.12, -0.87, 0.33, ...] ]
                ↓
        ┌────────────────────┐
        │  Vector Database   │
        │  (Stores vectors + │
        │   metadata)        │
        └────────────────────┘
                ↑
                │
        ┌────────────────────┐
        │   Query Input      │  ← (Text, image, etc.)
        └────────────────────┘
                ↓
        ┌────────────────────┐
        │  Embedding Model   │
        └────────────────────┘
                ↓
        [ Query Vector ]
                ↓
        ┌────────────────────────────┐
        │Approximate Nearest Neighbor 
         (ANN) Search
         (e.g., HNSW, IVF, LSH)    │
        └────────────────────────────┘
                ↓
        [ Most Similar Items Returned ]

This diagram shows how raw data is turned into embeddings, stored in a vector database, and then searched by meaning instead of keywords.

Why Are Embeddings So Powerful?

Because they:

Reduce complexity: Turn high-dimensional data (like images with thousands of pixels) into manageable vectors
Preserve meaning: Keep semantic relationships intact
Enable smart search and recommendations: Find things based on feeling, not just exact matches

Are embeddings universal? Is it same for all AIs ?

The short answer: No, embeddings are not universal.
Different AI models (from OpenAI, Google, Meta, Oracle, etc.) produce different embeddings for the same word or sentence.

Why Embeddings Differ

Different Training Data

OpenAI’s model might train on books, web pages, and code.
BioBERT (for bioinformatics) trains on PubMed papers.
Result: “cell” in OpenAI might be close to “jail,” while in BioBERT it’s closer to “protein.”

Different Model Architectures

Some embeddings are 512 numbers long, some 768, some 1536+.
Think of it like different “resolutions” of meaning.

Different Purposes

Domain-specific embeddings → trained for law, medicine, etc.

Sentence embeddings → capture whole meaning of a sentence.

Word embeddings → focus on single words.

Apple”
- In a general AI model (OpenAI) → vector is close to “fruit” and “company.”
- In a finance embedding model (BloombergGPT) → vector is closer to “NASDAQ,” “stock,” “earnings.”

So embeddings aren’t interchangeable across all AIs — they’re shaped by the model’s training data and goal.

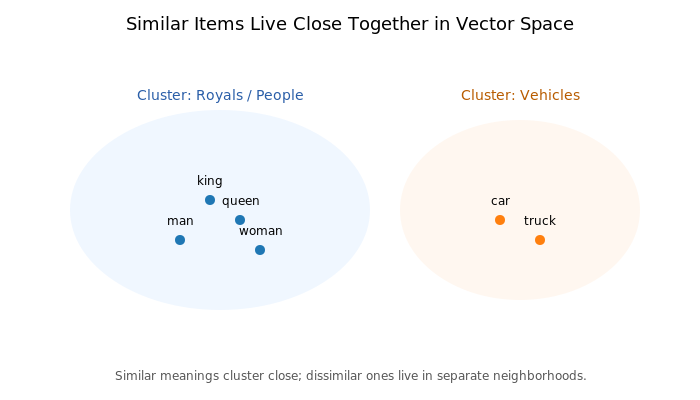
Similar Things Live Close in a Vector Database

One of the most fascinating ideas in vector databases is that similar things live close together. Let’s break down what this means.

When raw data—like text, an image, or even an audio clip—is passed through an embedding model, it is transformed into a long list of numbers (a vector). These numbers aren’t random. They are arranged in such a way that they capture the essence or meaning of the data.

For example:

The word “king” and the word “queen” will have vectors that sit close to each other.
An image of a dog and another image of a puppy will be closer in vector space than an image of a car.
A spoken phrase “good morning” will end up near the text phrase “hello”.

This closeness is measured using distance metrics like cosine similarity, Euclidean distance, or dot product. If two vectors point in nearly the same direction, the system interprets them as “similar.”

Now, why is this powerful? Because it means you don’t have to do exact keyword matching anymore. Instead, you can search by meaning. If you type “laptop bag,” the system can return results like “backpack for MacBook” even though the exact words don’t match—because the embeddings live close in the same region of the vector space.

In short:

Vector databases don’t just store data.
They store relationships of meaning, where similar items naturally cluster together.
This makes them essential for applications like recommendation systems, semantic search, chatbots, and more.

The Retrieval Process

Till now we have been discussing about the storage part – the embeddings. Lets switch to the retrieval part now. We will understand it stepwise:

Step 1: Imagine a Library

Think of your embeddings like tiny special “bookmarks” in a library.

Each document (page, paragraph, or sentence) you stored earlier is now sitting in the library as a vector (a list of numbers).
These numbers don’t look like words anymore, but they carry the meaning of the text.

Now, when someone asks a question (like “What are the health benefits of green tea?”), we need to find the bookmarks that are closest in meaning.

Step 2: Turning Question into Numbers

Just like we turned our documents into embeddings, we also turn the query (the question) into an embedding.

So now we have:

Stored embeddings = library of “bookmarks.”
Query embedding = a “bookmark” for the question.

Step 3: How Do We Compare Them?

This is where math comes in. Two common ways:

1. Dot Product

Imagine two arrows pointing in space (vectors).
The dot product measures how much they “point in the same direction.”
If they point in the exact same way → big dot product.
If they point in opposite ways → small or even negative dot product.

In retrieval, a bigger dot product = more similar meaning.

2. Cosine Similarity

Cosine similarity looks at the angle between two arrows.
If the angle = 0° (pointing exactly the same way) → cosine similarity = 1 (perfect match).
If the angle = 90° (pointing in totally different directions) → cosine similarity = 0 (no similarity).
If the angle = 180° (opposite directions) → cosine similarity = -1 (complete opposite).

In retrieval, we usually pick the embeddings with the highest cosine similarity.

3. Euclidean Distance

Imagine you have two arrows (vectors), but instead of checking how much they point in the same direction, you measure the straight-line distance between their tips.
- If the arrows are pointing in the same direction and are about the same length → small distance.
- If they’re pointing in different directions or have very different lengths → large distance.

In retrieval, we pick the vectors with the smallest Euclidean distance to the query.

Comparison of the Three

Let’s put them side by side using the arrow analogy:

Metric	What it Measures	When High/Low	Retrieval Rule
Dot Product	Overlap in direction and length	Bigger if arrows are long and aligned	Pick largest
Cosine Similarity	Angle between arrows (ignores length)	1 if same direction, 0 if orthogonal, -1 if opposite	Pick largest
Euclidean Distance	Straight-line distance between arrow tips	Small if arrows are close, large if far apart	Pick smallest

Why use one vs the other?

Cosine similarity → Great when you care about direction (semantic similarity, meaning). Usually best if embeddings are already normalized.
Dot product → Works well if embeddings carry useful information in their magnitude. Faster on hardware since ANN libs optimize for inner product.
Euclidean distance → Natural if your embedding space is designed like a coordinate system where closeness = smaller distance (common in clustering, image search, some ML tasks).

Example in simple terms

Imagine two arrows:

Query arrow: pointing northeast, length = 5.
Document arrow A: pointing northeast, length = 5.
Document arrow B: pointing north, length = 10.
Dot product → A is better (same direction & similar length).
Cosine similarity → A is better (angle = 0°, perfect).
Euclidean distance → A is better (they’re on top of each other), B is farther away in space.

Now if Document B pointed northeast too but was much longer:

Dot product might actually prefer B (because long arrows give a bigger dot product).
Cosine similarity would say A and B are equally good (direction only).
Euclidean distance would say A is closer (shorter straight-line gap).

✅ So the choice of metric depends on what “similar” really means in your application.

Text embeddings (like OpenAI’s) → cosine is usually the default.
Vector DBs → often use dot product because they normalize embeddings internally.
Clustering → Euclidean is common.

Step 4: Search Algorithms

Now, if your library has only 10 bookmarks, comparing one by one is easy.
But what if it has 10 million bookmarks? We need smart searching.

Some common search algorithms / techniques:

Brute Force (Exhaustive Search)
- Check similarity with every single embedding.
- Very accurate ✅, but slow ❌ for huge data.
Tree-Based Search (like KD-Tree or Ball Tree)
- Instead of checking everything, organize vectors into a tree.
- Cuts down the search space.
- Faster than brute force, but struggles in very high dimensions.
Approximate Nearest Neighbor (ANN)
- Sacrifices a little accuracy to gain a lot of speed.
- Algorithms like FAISS (by Facebook/Meta), HNSW (Hierarchical Navigable Small World graphs), Annoy, ScaNN do this.
- They don’t always find the exact nearest neighbor but usually find a “good enough” one very fast.

ANN uses cosine similarity/dot product/Euclidean inside its process to compare vectors.

Most vector databases (like FAISS, Pinecone, Weaviate, Chroma) use ANN under the hood.

Step 5: Putting It All Together

User asks a question → make a query embedding.
Compare query embedding with stored embeddings → using cosine similarity or dot product.
Use a search algorithm (brute force, KD-tree, or ANN) to find the top N closest matches.
Return those matches as the “retrieved documents.”

So, to understand these terms:

Embeddings = bookmarks.
Query = your own bookmark.
Cosine similarity / dot product = checking how much they “point the same way.”
Search algorithms = smart librarians who help you find the closest bookmarks quickly.

Wrapping It Up

When I first started exploring vector databases, I found myself struggling. Every course seemed to assume I already knew what embeddings were, or why vectors mattered, and I kept getting lost. That’s why I broke things down here with toys, candies, arrows, and libraries—the way I actually understood them.

If you’ve made it this far, you now have the foundation most courses skip. You understand:

What embeddings are (and why they’re like “flavor codes” for meaning)
How vectors capture similarity
How retrieval works through dot product, cosine similarity, and Euclidean distance

With this base, you can walk into any vector database course—FAISS, Pinecone, Weaviate, Chroma, or others—and move smoothly without that initial frustration I went through.

✨Remember: at its core, a vector database is not about scary math—it’s about capturing meaning and finding what’s truly similar.